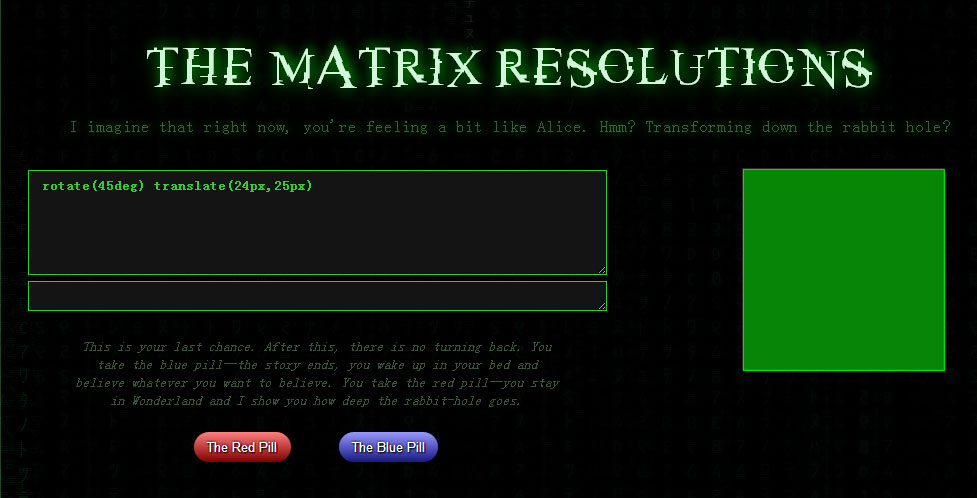
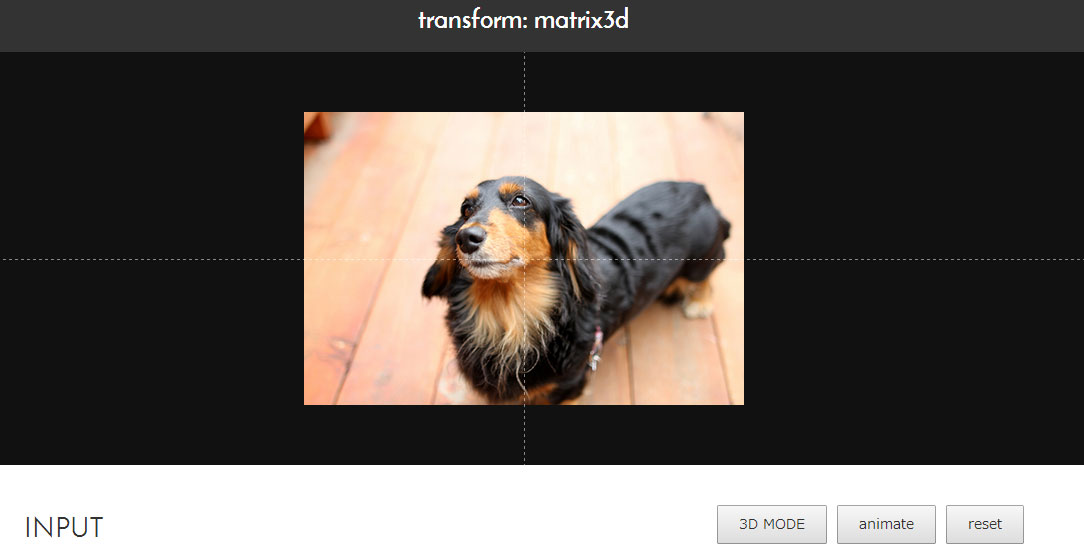
什么是Matrix?
Matrix(矩阵)是一个有关数字,符号,表达式组合的有趣的数学词汇,广泛应用于数学和科技领域。物理学家们还将其纳入量子力学的学习范畴。在电脑图形方面,它们被用于线性变形和处理3D图像和2D映画。Matrix 函数中的matrix()可以用来创建线性变化,matrix3d()可以用css在二维画面里创建三维图像。(下图是一个matrix例子)
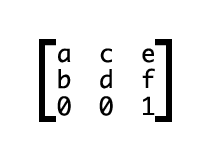
2D变换矩阵为3x3 ,3D变换则是4x4的矩阵;
矩阵(matrix)可以完成,斜拉(skew),缩放(scale),旋转(rotate)以及位移(translate);
变换矩阵基于一个特定坐标点相乘表示为一个向量。
坐标系统
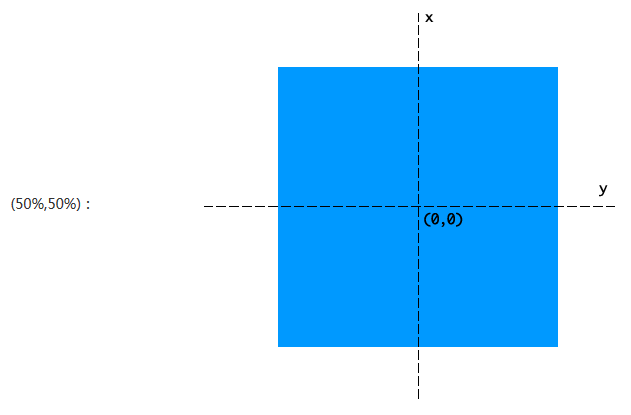
坐标系统。每一个文档视图都是一个坐标系统,左上角为视图的原点,坐标(0,0)。数值沿着X轴向右,沿着Y轴向下而递增。3D transform里面的Z轴决定了观察者所能觉察到的距离。数值越大,距离越近物象越大,数值越小,距离越远物象越小。
一个transform应用在一个对象上,就形成了一个当前坐标系统,坐标系的原点(0,0)默认位置在对象的中央。
2D坐标:
3D坐标:

transform 语法
它的所有语法如下图:
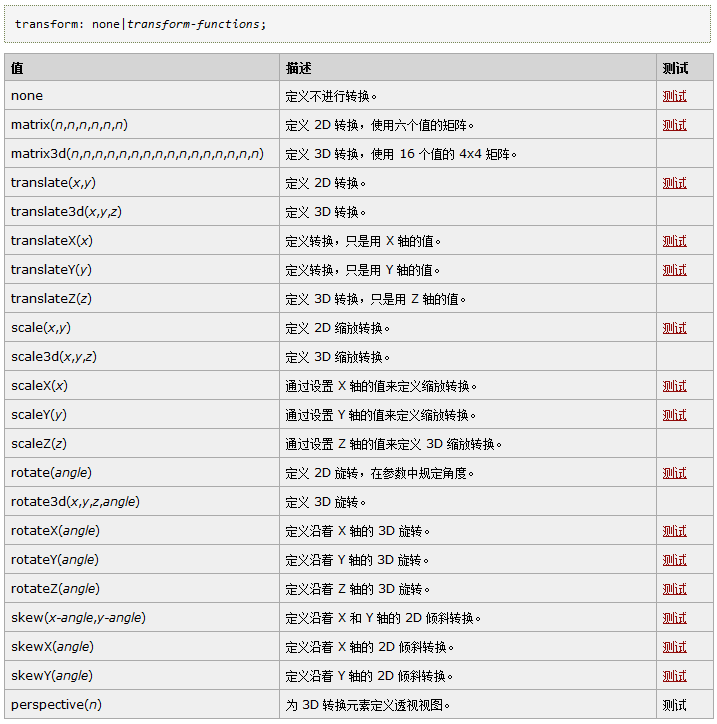
2D变换
矩阵等价函数
所有其他的CSS3变换函数等价的矩阵表示,看下图:
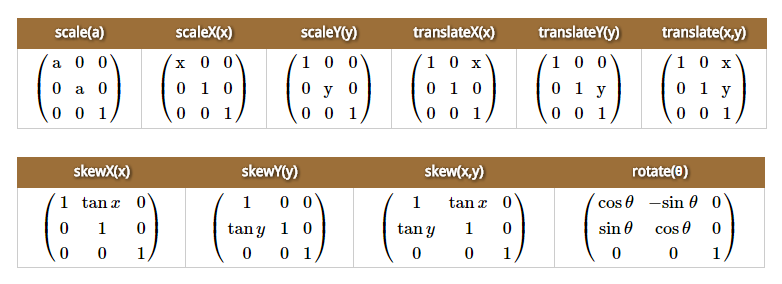
位移[translate]变换分解
该函数写法如下:
1
transform: matrix(a,b,c,d,e,f);
上面对应参数表示成矩阵是这样的:

现在我们让上边的矩阵变换一下,3x3矩阵每一行的第1个值与后面1x3矩阵的第1个值相乘,第2个值与第2个相乘,第3个与第3个,然后相加,过程如下:
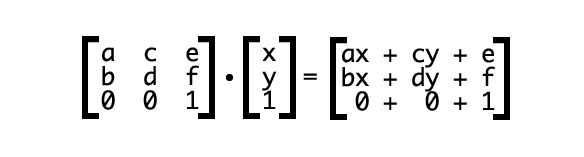
当我们应用一个2D tansfrom的时候,浏览器会把矩阵和一个向量([x, y, 1])相乘。x和y的值是当前坐标空间中特定的坐标点;
我们将每一列中的实体与向量中的列相乘得到最终的transform坐标;
此时ax+cy+e为变换后的水平坐标,bx+dy+f表示变换后的垂直位置。这样得出的一组数字和字符组合看起来毫无意义,但上文提到过,每一个transform都有一个矩阵:
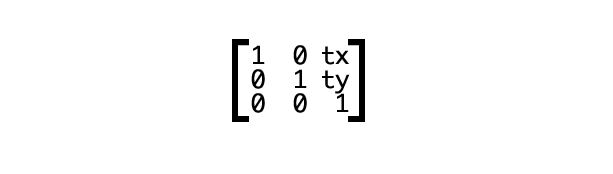
tx和ty的值就是要变形的数值,我们也可以用向量来表示:[1 0 0 1 tx ty]。向量可以看做是matrix() 的参数。把上面变换后的矩阵写成css代码就成了这样:
1
2
3
4.box{
transform: matrix(1, 0, 0, 1, tx, ty);
}从上边可以发,位移只要关心最后两个参数,公式如下:
1
2
3.box{
transform: matrix(与我无关, 与我无关,与我无关, 与我无关, 水平位移距离,垂直位移距离);
}
缩放(scale)
从matrix中的参数可以看到有两个数字1,对,这就是缩放相关的参数。
其中,第一个缩放x轴,第二个缩放y轴。写成公式:matrix(s, 0, 0, s, 0, 0),再套用上边的公式,就有:
x’ = ax+cy+e = sx+0y+0 = sx;
y’ = bx+dy+f = 0x+sy+0 = sy;
最后就是matrix(sx, 0, 0, sy, 0, 0);,等同于scale(sx, sy);
旋转(rotate)
旋转使用如下(假设角度为θ):
1 | matrix(cosθ,sinθ,-sinθ,cosθ,0,0) |
然后就有了:
1 | x' = x*cosθ-y*sinθ+0 = x*cosθ-y*sinθ |
使用matrix表示则还要计算cos, sin值,最简单的写法:
1 | transform:rotate(θ); |
拉伸(skew)
使用如下:
1 | matrix(1,tan(θy),tan(θx),1,0,0) |
然后就有了:
1 | x' = x+y*tan(θx)+0 = x+y*tan(θx) |
对应于skew(θx + “deg”,θy+ “deg”)这种写法。
1 | transform:skew(θx + "deg",θy+ "deg"); |
注:其中,θx表示x轴倾斜的角度,θy表示y轴
3D矩阵变换
matrix3d() 函数是一个3d变换函数是用来描述一个三维的序列 转换 在一个4×4的矩阵中。这是一个4x4的矩阵,sx , sy, sz代表了乘数的比例,如下:
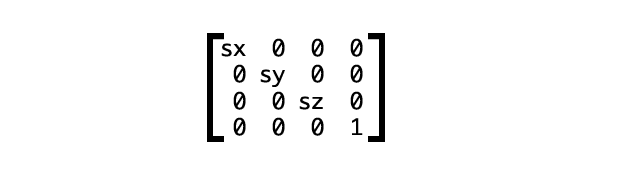
代码表示这样的:
1 | transform: matrix3d(sx, 0, 0, 0, 0, sy, 0, 0, 0, 0, sz, 0, 0, 0, 0, 1) |
从上可看出计算matrix3d()函数的值,不是很简单的,这要手工完成,那么也是很累的,也有人开发工具:
齐次坐标(homogeneous coordinates)
- 齐次坐标:所谓齐次坐标就是将一个原本是n维的向量用一个n+1维向量来表示。
- 向量:既有方向又有大小的量叫做向量(物理学中叫做矢量)。
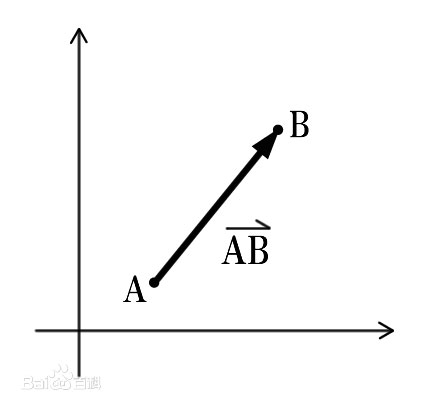
- 平面向量:平面向量是在二维平面内既有方向(direction)又有大小(magnitude)的量,物理学中也称作矢量,与之相对的是只有大小、没有方向的数量(标量)。平面向量用小写加粗的字母a,b,c表示,也可以用表示向量的有向线段的起点和终点字母表示。
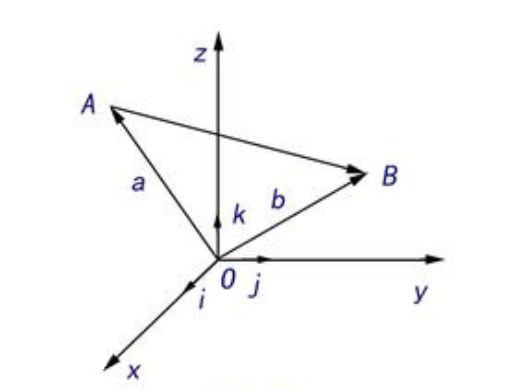
- 空间向量:空间中具有大小和方向的量叫做空间向量。向量的大小叫做向量的长度或模(moduius)。
在上面的矩阵中,我们可以看到平移的矩阵是相加的,而旋转跟缩放的矩阵都是相乘的,这样计算起来多麻烦呀!于是为了方便计算,大家都统一用一种方式来进行计算,聪明的计算机图形科学家,它们就设计出这样一种坐标系,叫齐次坐标(homogeneous coordinates),而它的目的只是为了更加方便地去用矩阵来计算图形的变换,没有其他。
那什么是齐次坐标呢?
其实就是在原来2D的维度,再加上一个新的维度,多出来的维度的值永远是1,比如点的矩阵就变成:
1 | ┌ ┐ |
而Translation(平移)的矩阵表示就变成:
1 | ┌ ┐ |
这样,平移变换的加法就可以变成乘法:
1 | ┌ ┐ ┌ ┐ ┌ ┐ |
Scale(缩放)跟Rotation(旋转)相对应的矩阵也就变成:
1 | ┌ ┐ ┌ ┐ |
注:引入齐次坐标的目的主要是合并矩阵运算中的乘法和加法。
浏览器支持情况
2D支持:
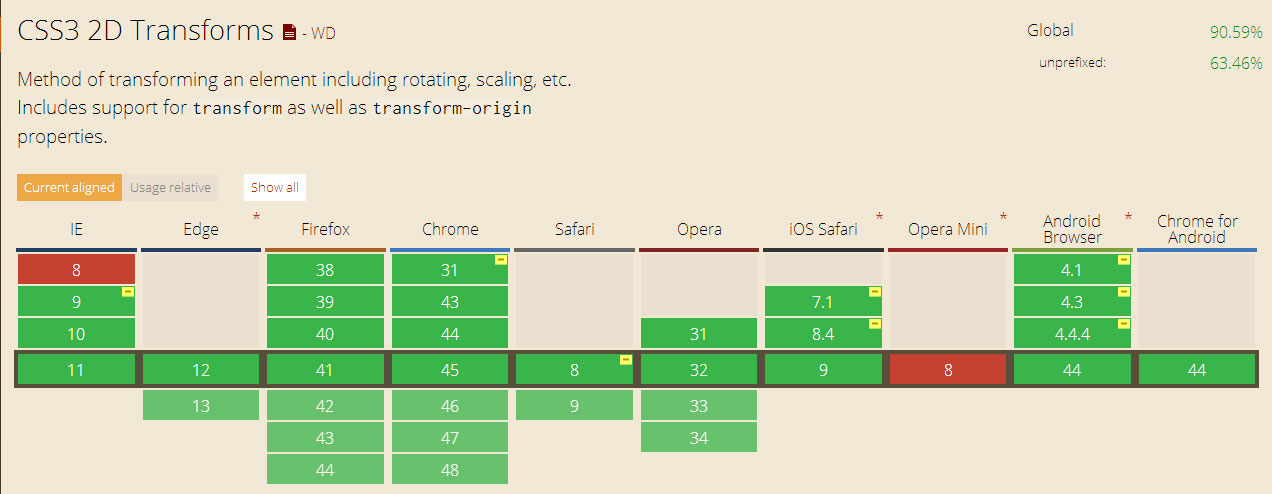
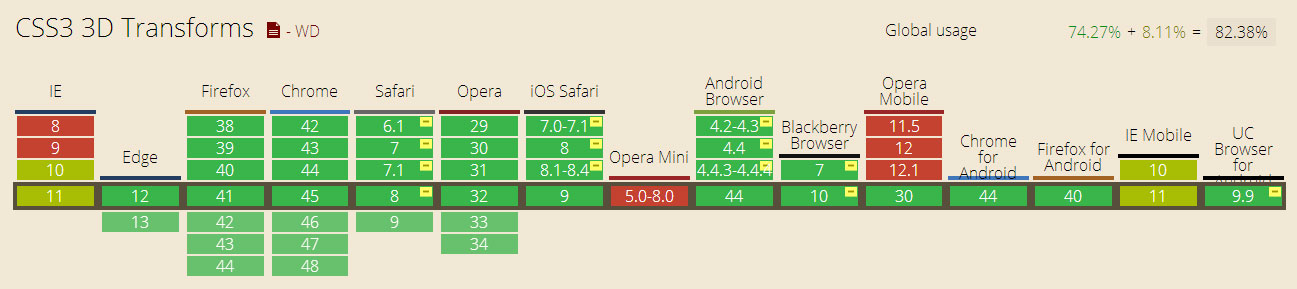
3D支持:
参考链接
- 张鑫旭-理解CSS3 transform中的Matrix
- [张鑫旭-CSS3 3D transform变换,不过如此!
- Dev.Opera-CSS Transforms Matrix-英文
- 最虾米-CSS3 Transform Matrix-中文
- Flash 中的变换矩阵
- codrops-Transform
- codrops-matrix3d
- MDN-transform
- w3school-CSS3 transform 属性
- Matrix (mathematics) from Wikipedia
- The CSS3 matrix() Transform for the Mathematically Challenged
- 2D平面中关于矩阵(Matrix)跟图形变换的讲解
- CSS3之3d transform
- CSS Transitions, Transforms & Animations – Perspective
- CSS3 Transform